This post summarizes the content and contributions of my recent paper leveraging simulation, prediction, and learning to achieve safety on complex systems via reduced order modeling, accepted and to be presented at the Conference on Learning for Decisions and Control held in Ann Arbor, Michigan in 2025. We first motivate the problem by highlighting the difficulties of achieving safety on complex systems. We then establish a theoretical basis to robustify a control barrier function derived on a reduced order model to achieve safety on the full order model, termed a Predictive Control Barrier Function. Finally, we present a learning algorithm, which improves real-time tractability and enhances sim-to-real transfer via domain randomization. We demonstrate the method on the hopping robot ARCHER.
The full text of the paper is available from on arXiv.
Problems with Safety on Complex Systems
When it comes to ensuring safety of complex robotic systems, it can be quite difficult to guarantee that a system remains within a desired invariant set. A key tool to ensure that systems remain safe is the control barrier function, which provides a condition on the input which, when satisfied, guarantees forward invariance of the desired set. With complex systems, synthesizing the function $h$ such that it is a valid control barrier function enforcing the desired safety criteria is quite a difficult problem; in general, complex relationships between the safety criterion and way the input enters the system can make this synthesis problem difficult or impossible.
In many cases, safety may depend only on a subset of the system states. For instance, in collision avoidance problems, safety can often be phrased to depend only on the system’s base position coordinates, and not on, say the configuration of the robot or its velocity. In this case, safe behaviors can be synthesized on a reduced order model, and these behaviors can be tracked by the full order systems. Previous works have treated the case where behaviors of the reduced order model can be tracked exponentially.
We aim to use a predictive horizon to consider a more broad class of tracking controllers, reducing assumptions on the tracking controller, and replacing them with data.
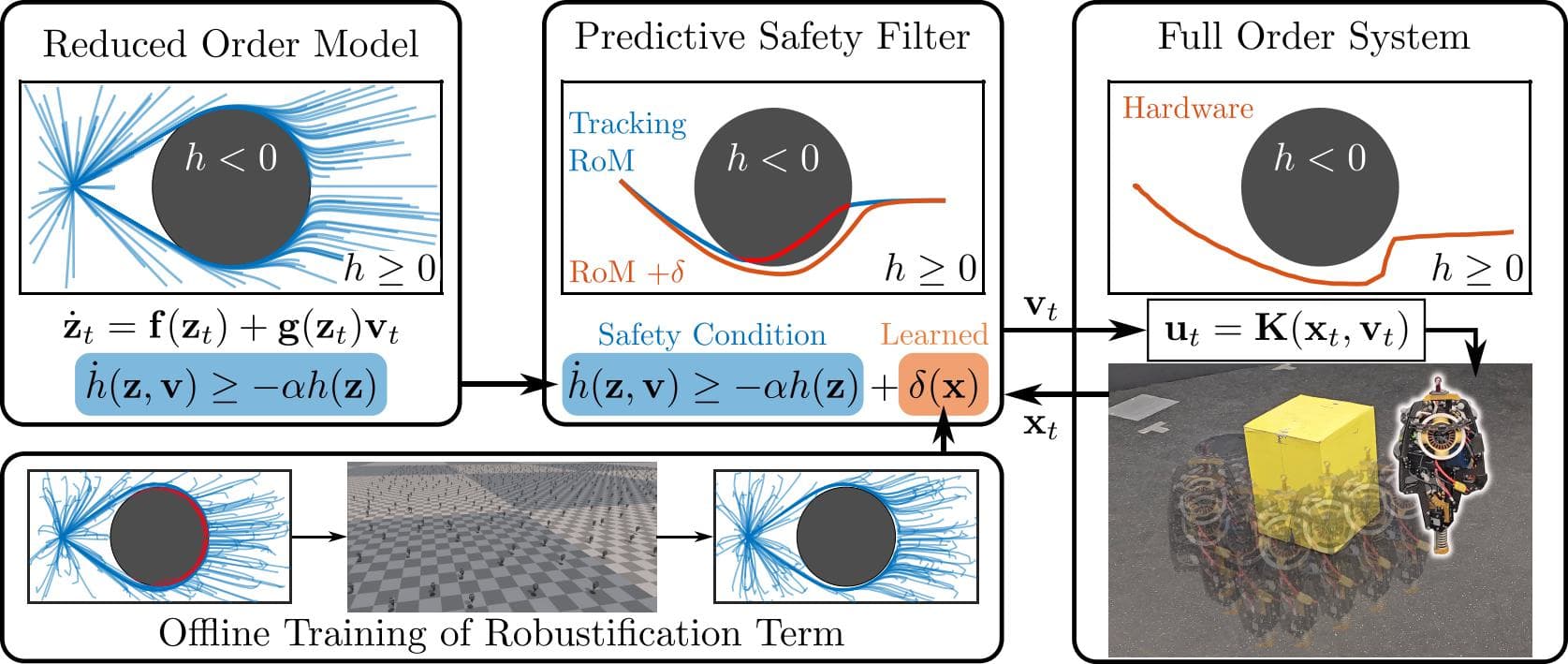
Predictive Control Barrier Functions (PCBFs)
The predictive CBF adds a minimal robustification term to ensure safety of the system, despite tracking error introduced by the layered architecture.
\(\delta(x) = \arg\min_{\delta >= 0} \delta \quad s.t.\) \(\dot{h}(\Pi(x_t),\dot{ x}_t) \geq -\alpha_{ x} h( \Pi( x_t))\) \(L_f h(z) + L_g h(z) v^{\delta}(z) \geq -\alpha h( z) + \delta\) \(\dot{ x}_t = F_{\mathrm{cl}}( x_t, K(x_t, v^{\delta}(\Pi(x_t)))\) we define the robustification term $\delta(x)$ to be the minimum constant such that when the reduced order model is executed robustified by this constant (second constraint, $v^\delta(z)$ being the robustified RoM input), and this behavior is tracked by the full order model (third constraint), the projection of the full order model onto the reduced order model remains safe, (first constraint).
We produce an algorithmic method for estimating this constant online, which iteratively increases or decreases an approximation of the constant in response to safety violations or buffers in a future horizon over a simulated rollout.
Learning Predictive CBFs
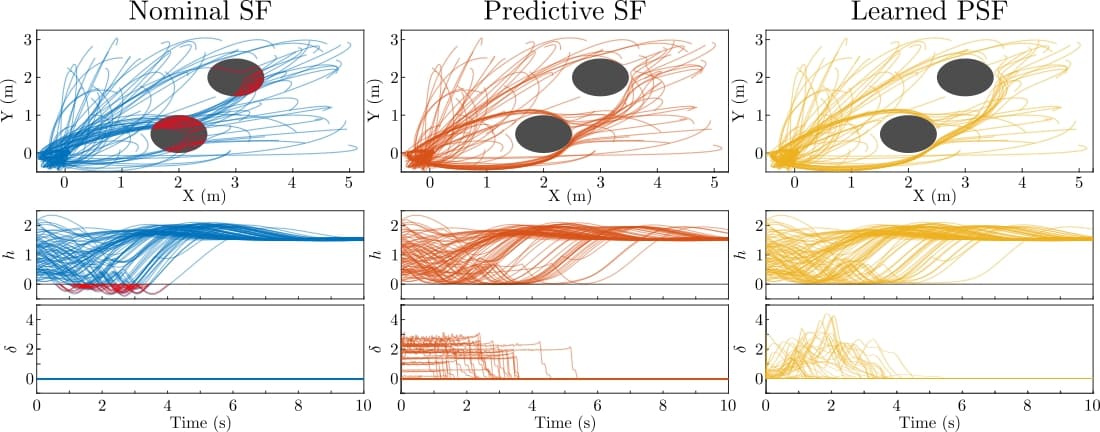
To amortize the amount of online computation, we can also parameterize $\delta^\theta(x)$ as a neural network with parameters $\theta$, and learn it as a function over the full order state space. We leverage parallel simulation of the layered safety filter in IsaacGym to produce massive amounts of training data in short time periods, allowing us to train these robustification terms efficently. The figure below compares the online method (predictive CBF) and learned method (learned PCBF) for a simple system where a double integrator tracks a single integrator.
Deploying PCBFs on the ARCHER Platform
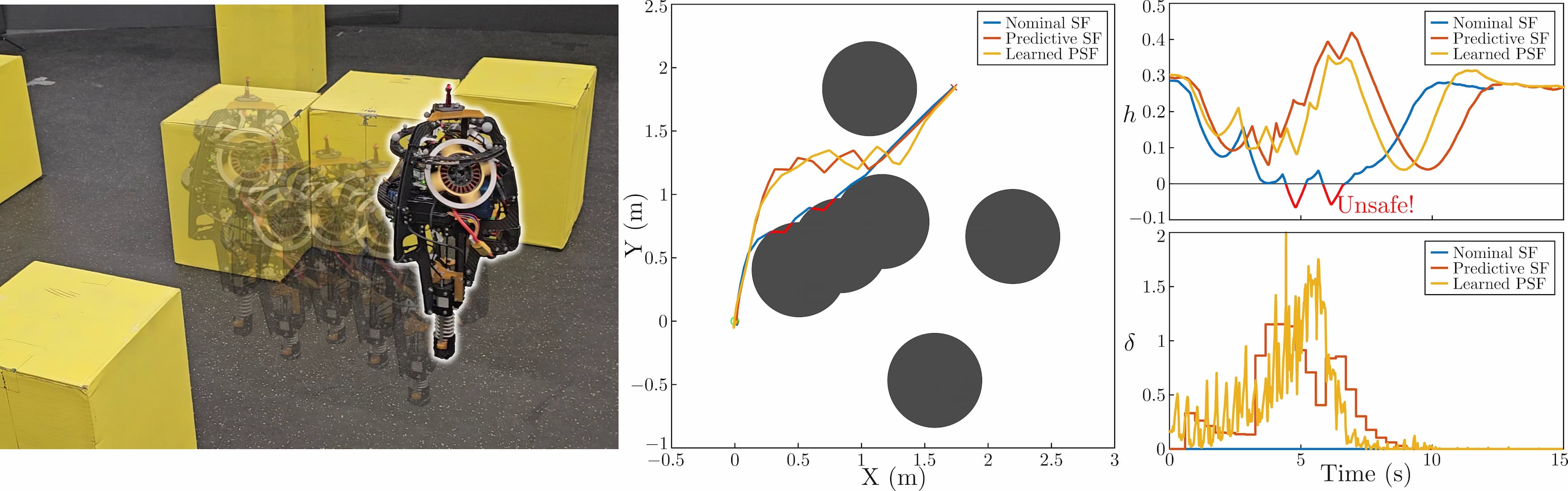
We deploy this method on the hopping robot ARCHER, using the tracking controller developed in our work on robust and agile hopping as the tracking controller. In experimental trials, we see a nominal safety filter failing, due to model mismatch with the single integrator used as a reduced order model, while both the predictive safety filter and learned predictive safety filter ensure safety on the hardware platform.
Conclusion
Predictive Control Barrier Functions (PCBFs) offer a powerful new way to guarantee safe control of complex systems by:
- Combining reduced-order modeling, predictive simulation, and learning.
- Enabling real-time, adaptive, and provably safe behaviors on challenging hardware platforms.