This post summarizes the content and contributions of my recent paper demonstrating robust and stable hopping on the robot platform ARCHER, accepted and presented at the International Conference on Intelligent Robots and Systems held in Abu Dhabi, United Arab Emerates in 2024. We first motivate the problem by highlighting the difficulties of controlling legged or hopping robotic systems. We then establish a zero dynamics policy, in the style of \cite{} (also discussed on my website), to stabilize the hopping robot. Finally, we demonstrate the effectiveness of this controller on ARCHER.
The full text of the paper is available from IEEE, or on arXiv.
Difficulties of Controlling Hopping Robots (ARCHER)
The hopping robot ARCHER contains a few key properties which makes it quite difficult to control using conventional methods from nonlinear control theory.
- The system is underactuated. There are no actuators on the position of the center of mass, so stabilizing the robot to a specific position requires careful coordination of the actuated degrees of freedom to stabilize the entire system.
- The system is hybrid. The system undergoes both continous and discrete (impact) dynamics, including two different continuous phases (flight and ground). Additionally, the ground dynamics are very stiff due to spring in the robot’s foot. These different dynamics modes can make planning and control and even simulation quite difficult compared to purely continuous or purely discrete systems.
- Tight input bounds. The motors on the flywheels have limited torque; input bounds can be difficult to treat with conventional nonlinear control methods.
- State-input constraints. Once the flywheels reach the maximum motor speed, they no longer can be used to apply torque to the robot in that direction. This represents a state-input bound (as inputs become bounded as flywheels approach saturation), which is even more difficult to handle than input bounds alone.
Hybrid Zero Dynamics Policies
We spend a good amount of time developing a rigorous formalism for zero dynamics policies in the context of hybrid systems, extending the work done in our treatment of continuous time zero dynamics policies. While I will leave the mathematical rigors to the paper, the conceptual idea for the zero dynamics policy, of which the Raibert Hueristic, commonly used since the 1980s to control hopping and walking robots, is a clear example.
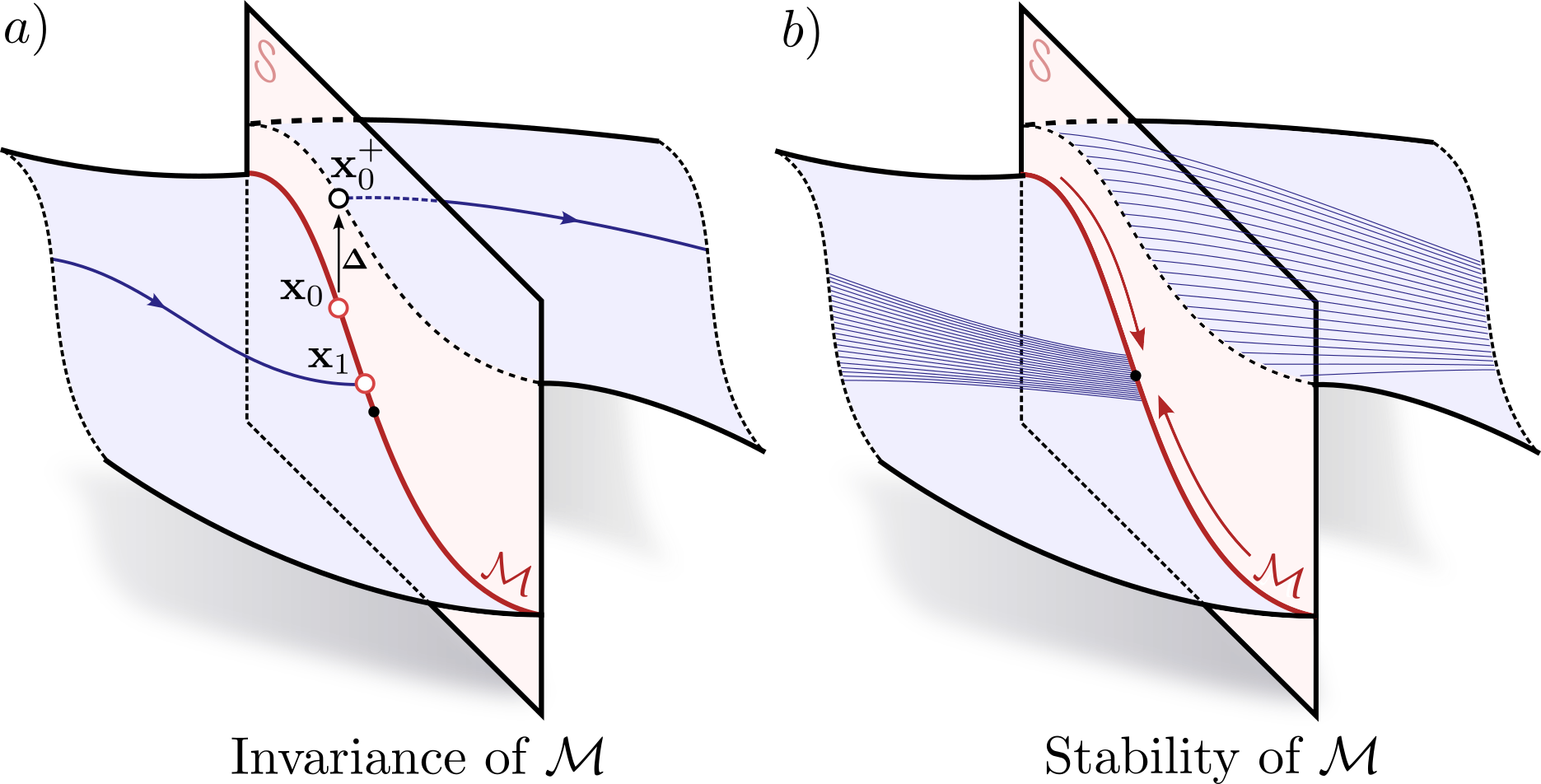
The zero dynamics policy is a map between the systems unactuated coordinates (in this case the position and velocity of the robot’s center of mass), to the actuated coordinates (in this case, the robots orientation, which is acutated by the flywheels). We we think about a pre-impact position for the hopping robot, with a given position and velocity of the center of mass, there is clearly a ‘best’ orientation for the system to be in - for instance, in the figure below, the hopper is left of the origin, and moving left; the desired orientation would have the foot well to the left of the center of mass, so the next hop moves back to the right.
If we connect up the ‘desired orientation’ at every position and velocity, we end up with a manifold, existing as a submanifold on the guard of the hybrid system. It turns out, as long as we can converge our orientation sufficently exponentially fast to this manifold, we stabilize the entire system to the origin. So during execution, we use a geometrically consistent PD controller to drive the hopper to a desired orientation, and stabilize the system to the origin in this manner.
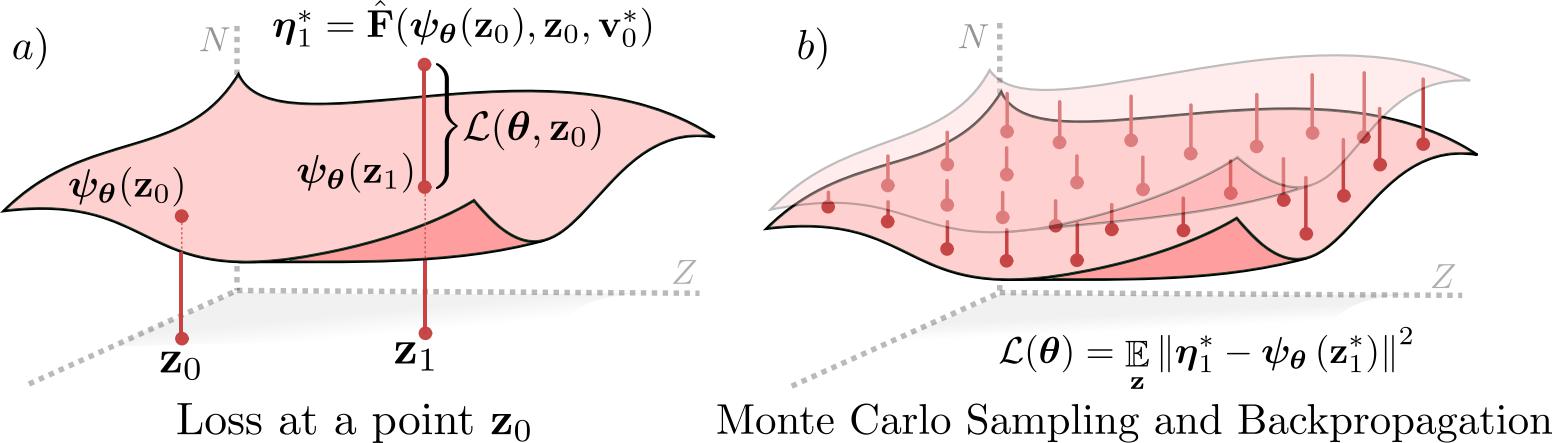
Finally, we develop a learning pipeline, shown above, which uses optimal control to learn this manifold for the hopper. While locally around the origin policies look similar to the Raibert Heuristic, they differentiate themselves with better behavior far from the origin.
Robust and Agile Stabilization of Hopping Robots (ARCHER)
The trained policy, shown in the above video, is quite capable of agile and robust hopping. It achieves several significant feats, including
- Over 3000 stable hops recorded during all experiments
- Robustness to signficant kicks and disturbances
- Blind traversal of steps and slopes over an obstacle course.
- “Walks the plank” across a 2x4 suspended two feet off the ground.
- Tightly tracks a square trajectory (shown below).
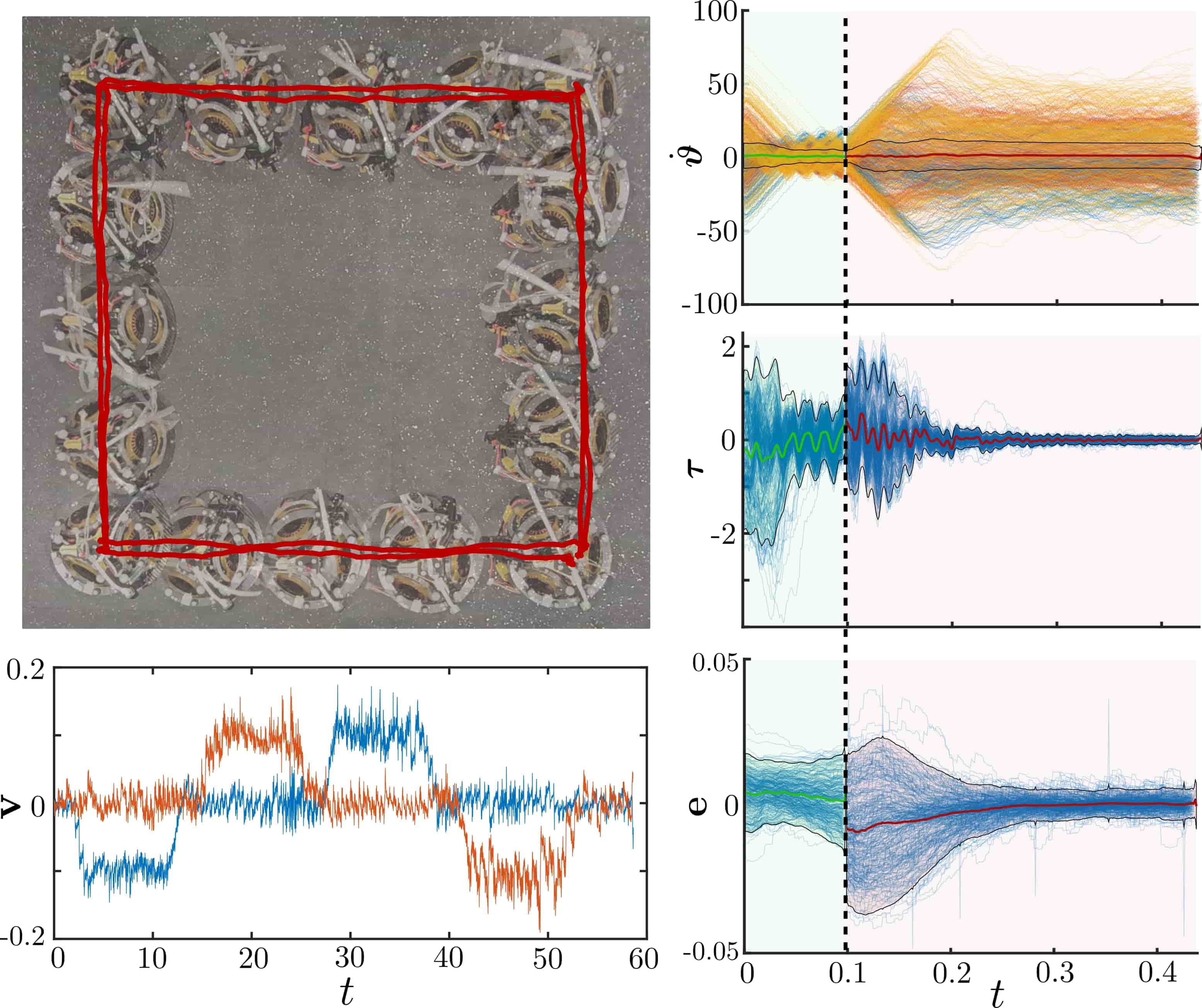 .
.
The above figure displays the flywheel speeds, torques, and orientation error on the right-side. A few critical peices of information can be gleaned; firstly, we see the orientation controller drives the error to zero, each hop. Secondly, note that the dotted line separates the ground phase (left of line) from flight phase (right of line). Note that flywheels speeds increase away from zero during the flight phase, as they are spun up to apply control torques. If left unchecked, this spinup would cause the flywheels to hit thier maximum speed, at which point the motors would saturate, and be unable to apply corrective torque. Critically, we apply a spindown controller in the ground phase, where instead of controlling orientation, the flywheels simply damp thier speed towards zero; this does not destabilize the orientation since during contact, the system’s effective inertia is much higher (measured about the contact point), compared with the flight phase (measured about the center of mass). Using this to maintain bounded flywheel energy, the hopper can hop as long as its battery power allows!
Conclusion
In this paper, we extend notions from continuous time zero dynamics policies to hybrid systems, and successfully deploy a learned zero dynamics policy on the hopping robot ARCHER. This policy achieves state of the art robustness and agility while hopping, including several impressive demonstrations included in the videos above.
